INTRODUCCIÓN
El diagnóstico precoz del cáncer de mama es fundamental para asegurar el mejor tratamiento y así aumentar la vida de las pacientes.
Existen muchas herramientas computacionales disponibles para administrar imágenes y conjuntos de datos. Un conjunto de datos muy conocido es el de cáncer de mama de Wisconsin(1) que se analizó para muchos estudios.
Algunos autores desarrollaron un modelo para la evaluación del riesgo de cáncer de mama y el diagnóstico temprano a partir del conjunto de datos mencionado anteriormente. Implementaron la selección de características de cáncer de mama usando análisis de los principales componentes (PCA) y la clasificación (riesgo y diagnóstico) usando máquina de vectores de soportes (SVM).(2) Otros autores utilizaron el mismo conjunto de datos y cinco clasificadores famosos como el árbol de decisión (DT), el vecino más cercano (KNN), la regresión logística (LR), Naïve Bayes (Gaussian NB) y SVM.(3) En otra publicación se midió el efecto de la reducción de la dimensionalidad utilizando el análisis de componentes independientes (ICA) en los sistemas de apoyo a la toma de decisiones de cáncer de mama con varios clasificadores, como la red neuronal artificial (ANN), el vecino más cercano 𝑘 (𝑘-NN), la red neuronal de función de base radial (RBFNN), y se investigó SVM.(4)
El objetivo de este estudio fue implementar las técnicas de reducción de dimensionalidad PCA y la escasamente utilizada kernel PCA para una mejor gestión de los datos. También otro objetivo fue clasificar los datos utilizando los algoritmos SVM y LR para analizar la ventaja de la reducción de las características.
MÉTODOS
La base de datos de cáncer de mama de Wisconsin utilizada contenía información de biopsias e información de los núcleos de las células. Contenía 569 muestras y 30 atributos (características) con 357 casos benignos y 212 casos malignos.
Se calcularon los atributos: radio, textura, perímetro, área, suavidad, compacidad, puntos cóncavos, simetría, dimensión fractal para cada núcleo celular de una biopsia.
Posteriormente se evalúo el valor medio, la desviación estándar (SE) y el peor o el mayor valor (valor medio de los tres valores más grandes) de los atributos calculados para cada imagen.
En este estudio se utilizó la plataforma Python Jupyter y se implementaron herramientas de Scikit-learn. El análisis del conjunto consistió en varios pasos, en primer lugar se observó la correlación de características utilizando la función de mapa de calor y se pudo encontrar una alta correlación entre algunas características.
El siguiente paso fue separar un 80 % del conjunto de datos (455 muestras con su clasificación) para entrenamiento del modelo (x_training, y_training) y un 20 % (144 muestras sin su clasificación) para pruebas del modelo (x_test, y_test) utilizando un valor de y_predicted. La calidad del modelo se evalúa obteniendo cantidades estadísticas significativas a partir de la comparación del y_test con respecto al y_predicted. Posteriormente estos valores fueron utilizados en la etapa de clasificación.
Se implementaron los algoritmos PCA(5) y Kernel PCA para reducir la dimensión de los atributos (eran 30) a 2, 4 y 6 con el objeto de facilitar el manejo de los datos, pero sin pérdida de información. Se normalizó el conjunto de datos de entrenamiento y de prueba con una función gaussiana, utilizando la función StandardScaler.
Los algoritmos PCA y kPCA fueron obtenidos desde la librería de Phyton de Scikit-learn. Dichos algoritmos fueron solamente aplicados a las variables x_training, x_test.
Se elaboró un gráfico de porcentaje de variación de la varianza explicada para las 6 componentes principales y un mapa de calor para 2, 4 y 6 componentes principales. También se realizó un gráfico de la visualización del subespacio reducido con 2 componentes principales para PCA y kPCA (polinomio kernel y grado dos).
Una vez que los datos fueron procesados se procedió a seleccionar dos algoritmos lineales, SVM(6) y LR, para realizar aprendizaje de máquina supervisado. En esta parte se clasificaron los datos.
La selección de los mejores hiperparámetros de los algoritmos SVM y LR se realizó con una función de validación cruzada, GridSearchCV, para el conjunto de entrenamiento con 30 características, con las siguientes consideraciones:
Para SVM se utilizó una grilla de parámetros:
{'C': [1, 10, 100, 1000], 'kernel': ['linear']}, {'C': [1, 10, 100, 1000], 'gamma': [0.001, 0.0001, 1, 10, 100], 'kernel': ['rbf']}, {'C': [1, 10, 100, 1000], 'degree': [1, 2, 3, 5, 7], 'kernel': ['poly']}].
Para LR, la grilla de parámetros usada fue:
[ {'solver' : ['newton-cg', 'lbfgs'], 'C': [0.001, 0.01, 0.1, 1, 10, 100, 1000], 'penalty': ['none', 'l2']}, {'solver' : ['liblinear'], 'C': [0.001, 0.01, 0.1, 1, 10, 100, 1000], 'penalty': ['l1']}]
Se calcularon los valores de las métricas: exactitud, precisión, exhaustividad, F1 y AUC (área bajo la curva) y también se obtuvo la matriz de confusión para cada caso.(3)
Según los mejores hiperparámetros, se llevó a cabo la clasificación para los componentes PCA y kPCA 2 y utilizando el conjunto de entrenamiento, para PCA y kPCA para 2, 4, 6 componentes principales utilizando el conjunto de pruebas - transformado con la reducción de dimensión. El mejor modelo se encontró analizando las métricas. También se construyó la función de decisión. Finalmente, se compararon los resultados de la clasificación en el espacio latente con la misma clasificación en el espacio de entrada original.
La clasificación se realizó con SVM y herramientas de regresión logística. Se llevó a cabo una validación cruzada para seleccionar los mejores hiperparámetros de esos modelos, con el conjunto original y con el conjunto de dimensión reducida. Se transformaron los datos de testing con la reducción de dimensión aprendida en el primer paso. Luego se aplicó la función de clasificación aprendida en el paso anterior. Finalmente se determinó el mejor modelo en función de las métricas evaluadas previamente.
También se compararon con trabajos realizados por diferentes autores.
RESULTADOS
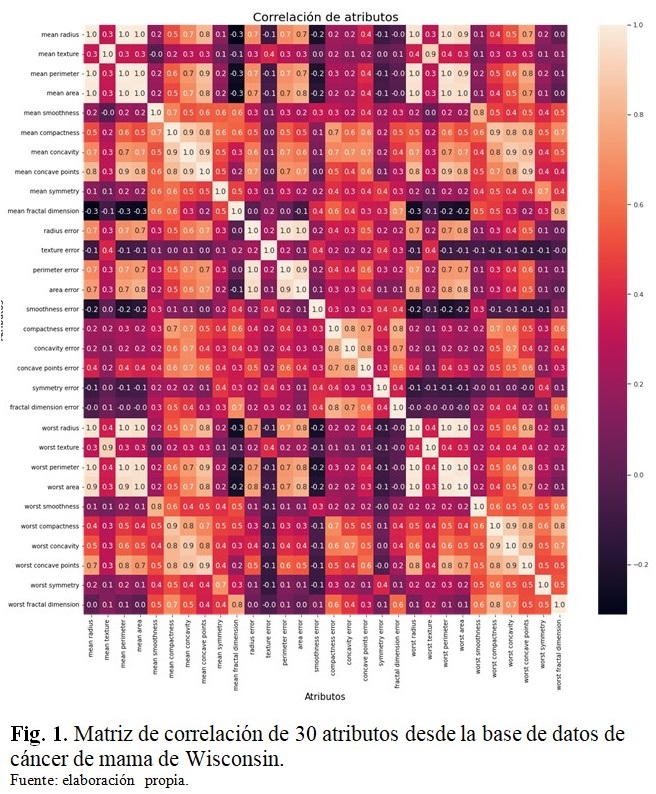
Es importante observar la matriz de correlación para comprobar si algunas características contienen la misma información. En la Figura 1 se muestra la matriz de correlación con los 30 atributos o características. (Fig. 1).
Por otro lado, se estudió el porcentaje de variación explicada para 1 - 6 componentes principales y se observó que 2 componentes tenían una razón de varianza explicada de 64 %, 4 componentes un 80 % y 6 componentes un 90 %, aproximadamente.
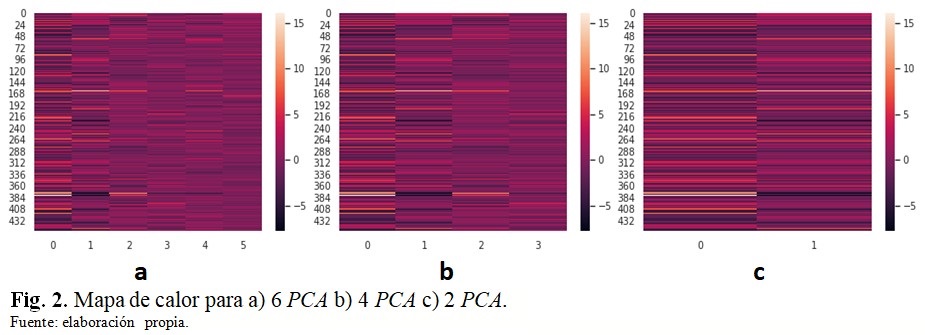
En la figura 2 se muestran diferentes mapas de calor (x-train preprocesado usando StandardScaler) para a) 6 PCA, b) 4 PCA y c) 2 PCA. Esta es otra forma de analizar cómo la varianza se explica para 2, 4 y 6 componentes principales. (Fig. 2).
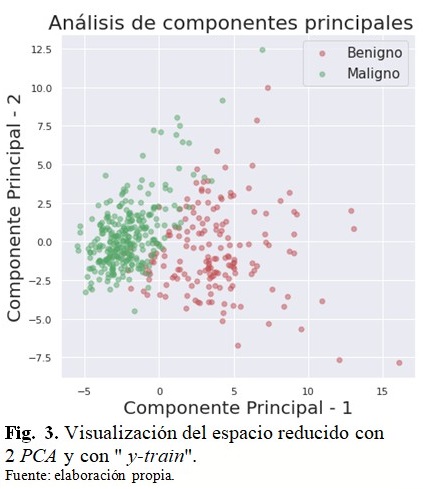
En la figura 3 se muestra la visualización del subespacio reducido para 2 componentes principales con las muestras de color rojo correspondientes a lesiones malignas y de color verde a lesiones benignas. Con los datos transformados por PCA se logran separar las 2 clases o sea las lesiones malignas de las benignas, mediante un hiperplano. (Fig. 3).
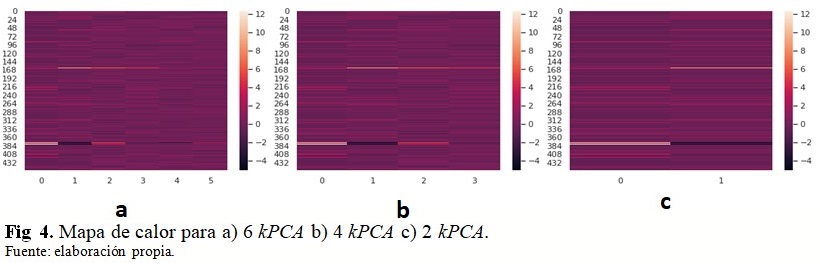
La figura 4 muestra los mapas de calor para a) 6 kPCA b) 4 kPCA c) 2 kPCA y se observa cómo la varianza se explica por 6, 4 y 2 componentes. La mayor variación de información se mostró para 2 y 4 componentes. (Fig. 4).
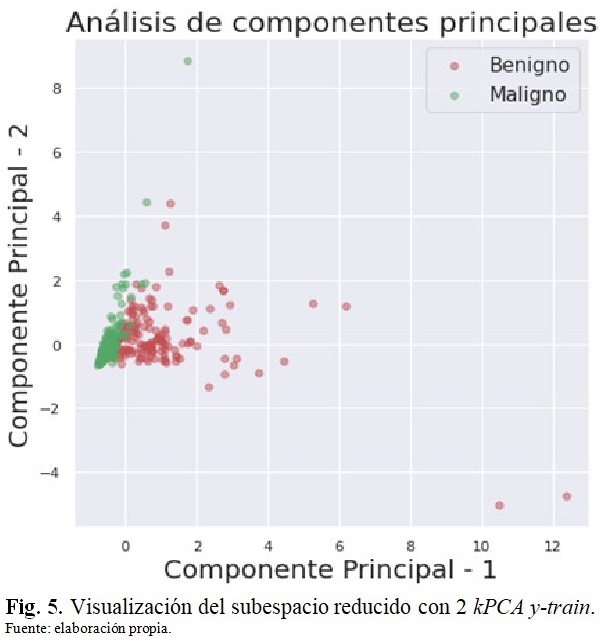
En la figura 5 se muestra la visualización del subespacio reducido con 2 componentes principales (2 kPCA) con las muestras de color rojo y verde correspondientes a lesiones malignas y benignas, respectivamente. (Fig. 5).
Después de aplicar las técnicas de PCA y kPCA, se realizó una validación cruzada para encontrar el mejor hiperparámetro para SVM y LR. Para el algoritmo SVM fueron: kernel linear y C = 100 y para el algoritmo LR fueron C = 100, solver Newton-cg e I2.
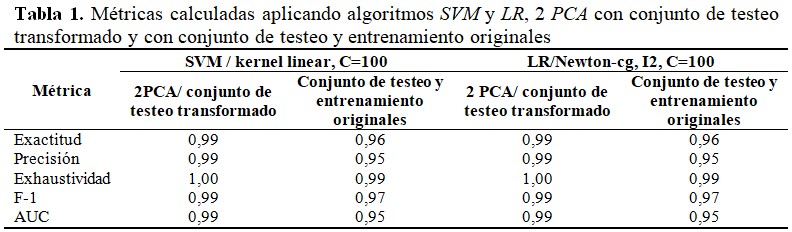
La tabla 1 muestra los valores de las métricas de SVM y LR para 2 PCA con un conjunto de pruebas transformado y un conjunto de pruebas y entrenamiento original. Se obtuvieron los mejores valores de las métricas cuando se utilizó el conjunto de prueba transformado. (Tabla 1).
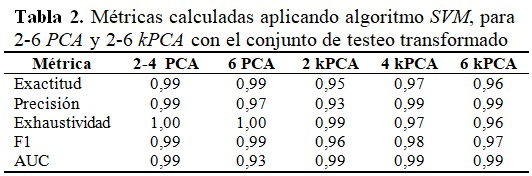
En la tabla 2 se muestran las métricas estadísticas para el algoritmo SVM, para 2-6 PCA y 2-6 kPCA utilizando un conjunto de pruebas transformado. Los mejores resultados de las métricas estudiadas fueron para 2 - 4 PCA. (Tabla 2).
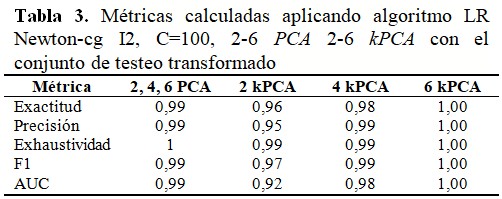
En la tabla 3 se muestran los valores de las métricas obtenidas aplicando LR Newton-cg I2, C = 100, 2-6 PCA 2-6 kPCA con valores de prueba transformados. Los mejores resultados de las métricas estudiadas fueron para 6 kPCA y para 2, 4, 6 PCA. (Tabla 3).
También se obtuvo matriz de confusión para 2 kPCA, b) 4 kPCA c) 6 kPCA utilizando el algoritmo LR.
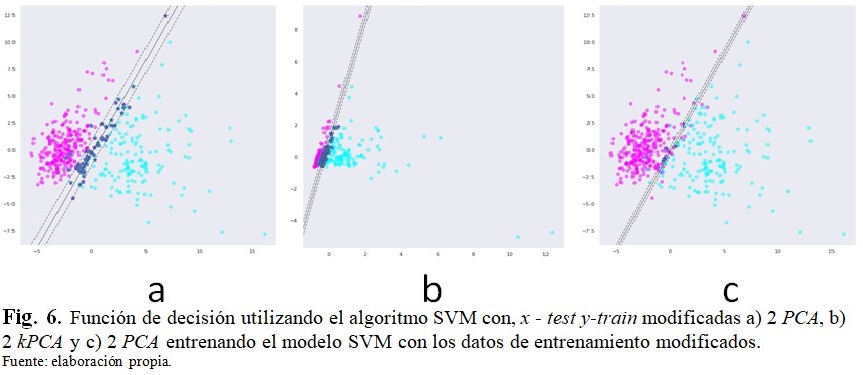
La figura 6 muestra la función de decisión (hiperplano), con sus correspondientes márgenes, utilizando el algoritmo SVM como clasificador y con el conjunto de pruebas transformado a) 2 PCA, b) 2 kPCA y c) 2 PCA entrenando el modelo SVM usando los datos de entrenamiento modificados. (Fig. 6).
DISCUSIÓN
En la matriz de correlación se observó que hay varias características que tienen la misma información y podrían reducirse, por ejemplo, el caso de la peor concavidad, la peor compacidad y los peores puntos cóncavos.
También se estudió el porcentaje de la variación explicada para 1 - 6 componentes principales y los valores calculados fueron elevados, por lo cual, a partir de dicha información se podría aplicar satisfactoriamente el algoritmo PCA y kPCA. Esta misma conclusión se dedujo desde la observación de los mapas de calor para 6 PCA, 4 PCA y 2 PCA. La mayor variación de información se mostró para 2 PCA.
Cuando se graficaron la 2 PCA versus 1 PCA, se pudo observar que, efectivamente, con los datos transformados por PCA se logran separar las 2 clases o sea las lesiones malignas de las benignas, mediante un hiperplano. Entonces, a partir de esto se podría aplicar algún algoritmo tipo SVM, LR u otro para la clasificación. (Tener en cuenta que cada componente representa una combinación de algunas características.)
El análisis explicado previamente se repitió para el algoritmo kPCA y en los mapas de calor para 6 kPCA, 4 kPCA y 2 kPCA, se observó la mayor variación de información para 2 y 4 componentes. En tanto que en la visualización del subespacio reducido con 2 componentes principales también se observó que con un hiperplano podrían separarse las dos clases de lesiones, malignas y benignas.
Cuando se aplicaron los algoritmos SVM y LR para 2 PCA con un conjunto de pruebas transformado y un conjunto de pruebas y entrenamiento original, se obtuvieron los mejores valores de las métricas cuando se utilizó el conjunto de prueba transformado.
Por otro lado, cuando se aplicó el algoritmo SVM con los mejores hiperparámetros calculados para 2 - 6 PCA y 2 - 6 kPCA utilizando un conjunto de pruebas transformado, se observó que los mejores resultados de las métricas estudiadas fueron para 2 - 4 PCA.
Cuando se aplicó el algoritmo LR, con los mejores hiperparámetros calculados, para 2 - 6 PCA y 2 - 6 kPCA con valores de prueba transformados, se observó que los mejores resultados de las métricas estudiadas fueron para 6 kPCA y para 2, 4, 6 PCA.
Del análisis de matriz de confusión para 2 kPCA, b) 4 kPCA c) 6 kPCA utilizando el algoritmo LR, se observó que la mejor matriz encontrada fue para 6 kPCA.
Los resultados obtenidos en este trabajo, para PCA con los algoritmos de clasificación SVM y LR, están de acuerdo con los de Galarza Hernández,(7) y levemente mejores con respecto a los resultados de Mushtaq et. Al.(3)
En la última parte de este trabajo se graficó la función de decisión obtenida usando el algoritmo SVM con el conjunto de pruebas transformado 2 PCA, 2 kPCA y 2 PCA entrenando el modelo SVM usando los datos de entrenamiento modificados. Para la primera figura se observaron márgenes amplios, significando que hay muchos puntos mezclados, en tanto que para la última figura se ve que los márgenes son muy delgados, menos puntos mezclados. Para la segunda figura, aunque los puntos están más compactados se puede ver que la clasificación sería muy buena. También se puede ver cómo las pendientes de los hiperplanos, rectas, son diferentes para cada caso.
Se puede concluir que en este estudio se aplicaron las técnicas PCA y kPCA y los algoritmos SVM y LR para el diagnóstico de los datos de la base de cáncer de mama de Wisconsin. Se encontró que la exactitud, precisión, exhaustividad, F1 y las AUC se pueden mejorar considerablemente aplicando los siguientes pasos:
• Normalización de las características.
• Reducción de dimensionalidad.
• Validación cruzada.
• Optimización de hiperparámetros.
Los mejores resultados de clasificación se alcanzaron para PCA 2, 4 y para 6 kPCA empleando los algoritmos SVM y LR, respectivamente. Por lo tanto, trabajar en el espacio latente mejoró las puntuaciones de las métricas. También los resultados de PCA con SVM y LR coinciden con valores de bibliografía.
En el futuro se podrían utilizar más métricas y se podrían usar otras bases de imágenes/datos.
Agradecimientos
A los profesores y compañeros del doctorado de la Universidad Tecnológica Nacional por siempre estar dispuestos a colaborar con sus pares.
Conflicto de intereses
No existen.
Contribuciones de los autores
Conceptualización: Rosana Pirchio.
Curación de datos: Rosana Pirchio.
Análisis formal: Rosana Pirchio.
Investigación: Rosana Pirchio.
Metodología: Rosana Pirchio.
Visualización: Rosana Pirchio.
Redacción del borrador original: Rosana Pirchio.
Redacción, revisión y edición: Rosana Pirchio.