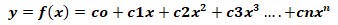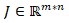INTRODUCCIÓN
El Banco de Sangre Provincial de Cienfuegos, perteneciente al Ministerio de Salud Pública, es una institución establecida en esta provincia desde el año 1965. En 1988 fue inaugurada una nueva instalación mucho más funcional que la existente hasta ese momento. Cuenta con el equipamiento necesario para realizar sus producciones con eficiencia, seguridad y calidad. Un equipo de profesionales altamente competentes, integrado por médicos y tecnólogos especializados en medicina transfusional y laboratorio clínico y otros profesionales de diferentes ramas del saber, conforman el capital humano de la institución.(1)
El Banco de Sangre cuenta con salón de espera para los donantes y comodidades para la extracción de sangre y plasma por aféresis automatizada; área para el procesamiento de la sangre o elaboración de componentes sanguíneos y/o suero; cuenta con un equipamiento necesario para realizar sus producciones con gran eficiencia y calidad. Posee, además, laboratorios como el de Inmunohematología, Seroepidemiológico, Clínico y Control de calidad Físico – Químico y Microbiológico, que cumplen con las regulaciones establecidas por el MINSAP y hacen posible que sus productos tengan una gran seguridad. Posee unidades móviles que acercan los servicios al donante, a través de las visitas a los distintos municipios de la provincia.(2)
El consumo de electricidad del banco de sangre de Cienfuegos se rige por la Resolución 299 del MINSAP que norma el consumo eléctrico, a nivel nacional, de los Bancos de Sangre (7.56 kW por donaciones).
El Programa Nacional de Sangre posee 46 Bancos, de ellos 15 provinciales, 31 municipales y 168 centros de extracción de sangre, aseveró a la AIN la doctora Ester Porto González, jefa del Programa Nacional de Sangre, del Ministerio de Salud Pública (MINSAP).(3)
El Día Mundial del Donante de Sangre se celebra cada 14 de junio en honor al nacimiento del doctor austríaco Kart Landsteiner, descubridor de los grupos sanguíneos humanos y Premio Nobel de Fisiología y Medicina en 1930.
Cuba se suma a tan importante celebración con 400 000 donaciones voluntarias anualmente, lo que demuestra el humanismo de esas personas y ofrece, además, una respuesta a las necesidades de las instituciones hospitalarias y a la producción de medicamentos.(3)
El objetivo de este trabajo es elaborar un modelo estadístico - matemático para determinar el número de donantes de sangre que minimicen el consumo de energía eléctrica en el Banco de Sangre de Cienfuegos y cumpla con los planes de la institución.
MÉTODOS
En el trabajo se halla la relación entre las donaciones, variable independiente (y) y el consumo de electricidad, variable dependiente de las donaciones (x), en los 5 años en Cienfuegos.
Se utilizaron modelos estadístico - matemáticos para obtener el modelo de regresión no lineal y compararla con la norma cubana de donaciones para poder llegar al número de donaciones diarias a realizar en el Banco de Sangre que minimice el consumo de electricidad. Con el modelo estadístico - matemático obtenido se hacen los análisis pertinentes para días de alta asistencia mantener las donaciones y minimizar el consumo eléctrico, en los días de poca asistencia de donantes se explica la importancia de la utilización del modelo estadístico -matemático empleado.(4)
Para la obtención de los objetivos del presente trabajo, se presentan los siguientes pasos, en el cálculo del modelo estadístico – matemático:
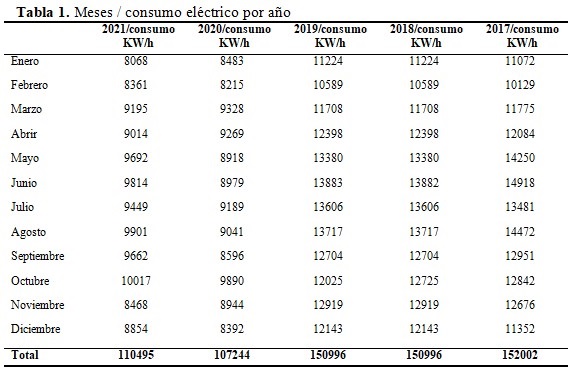
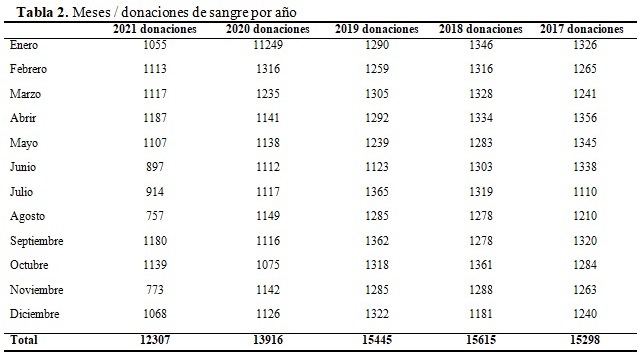
a. Obtención de los datos para el cálculo del modelo de predicción de arribo de donantes y el consumo energético obtenido, correspondientes al período (2007-2021). La base de datos utilizada se presenta en las tablas: Tabla 1 (Meses por año/consumo energético) y Tabla 2 (Meses por año / donaciones de sangre), para el período estudiado. (Tabla 1 y Tabla 2).
b. Cálculo del Modelo de correlación entre las donaciones y el consumo eléctrico y comparación con la norma cubana del MINSAP.(5)
c. Se prueba el supuesto de que el consumo de energía eléctrica no se comporta de manera lineal esperada con respecto a la cantidad de donaciones que se producen por mes, prueba de correlación lineal que mide la relación entre dos variables.(6)
En caso de no estar altamente correlacionadas se pondría de manifiesto que la cantidad de donaciones no estaría influyendo en el consumo.(7) Se realiza de Prueba de Kruskal-Wallis sobre la variable “y” y los tratamientos de “g”.(8)
d. Se aplica la prueba de comparación de múltiples rangos Dunn utilizando el ajuste del p-value Bonferroni, se obtienen los pvalues de cada combinación de tratamiento de “g” tomados dos a dos.
e. Cálculo de la ecuación no lineal de regresión entre la donación de sangre y el consumo energético por mes. Método de los Mínimos Cuadrados.
f. Modelo computacional para calcular el rango de donaciones con menor consumo energético.
RESULTADOS
Se analizan los datos mensuales de las Tablas 1 y Tabla 2 que presentan registros
60 observaciones en el período de 5 años (2017-2021):
Se declaran las siguientes variables en el análisis:
t: Fecha en la cual se realiza la mediación.
X: Cantidad de donaciones que se realizan mensualmente. Variable cuantitativa discreta medida en escala de razones. Variable independiente.
Y: Consumo mensual eléctrico del centro dado en kw/h. Variable cuantitativa continua medida en escala de razones. Variable dependiente.
g: Variables discreta en clases, que representa los tratamientos referentes a la cantidad de donaciones mensuales. Cuenta con los tratamientos que son las donaciones divididas en 3 clases (1: menos de 1200 donaciones, 2: entre 1200 y 1300 donaciones y 3: más de 1300 donaciones.)
Los tratamientos se agrupan en las siguientes cantidades de registros:
Tratamiento 1: 24 registros (40 %)
Tratamiento 2: 18 registros (30 %)
Tratamiento 3: 18 registros (30 %)
Una ecuación lineal de ajuste entre las donaciones de sangre y el consumo energético Y = a + b X, no presenta significación estadística.
El coeficiente de correlación lineal entre ambas variables fue 𝜌 = 0.48, esto pone de manifiesto que las variables presentan una correlación lineal directa muy débil y es preciso ir a regresión no lineal para poder explicar el comportamiento del consumo energético Y en relación al número de donaciones de sangre X.
Al aplicar la prueba de Kruskal-Wallis, se obtuvo un p-value menor que 0,05 lo cual pone de manifiesto que existe evidencia estadística para concluir que hay diferencias en relación a los tratamientos de la variable “g”, en al menos un grupo con respecto al resto. (Tabla 3).
Aplicando la prueba de comparación de múltiples rangos, utilizando el ajuste del p-value Bonferroni, se obtienen los p-values de cada combinación de tratamiento de “g” tomados dos a dos. En esta tabla se pone de manifiesto la conformación de dos clases bien definidas, las cuales han quedado conformadas de acuerdo a los resultados obtenidos.
En la Tabla 4 se expone, de manera resumida, la pertenencia de cada tratamiento de “g” a las clases conformadas. Se han conformado tres clases: a, b y c. La clase a se encuentra integrada por los tratamientos de cantidad de donaciones: “menores de 1200”, la clase b la forman tratamientos de cantidad de donaciones “entre 1200 y 1300” y la clase c tratamientos de donaciones “mayor de 1300”.
Se pone de manifiesto que el consumo eléctrico no presenta cambios estadísticamente significativos cuando la cantidad de donaciones es mayor que 1200 por mes, clases b y c. Sin embargo, la clase a se encuentra integrada por el tratamiento de cantidad de donaciones: “menor 1200” lo cual indica que el consumo mensual de corriente es significativamente menor cuando la cantidad de donaciones no llega a 1200. (Tabla 4).
Se aplicó la Prueba de Shapiro-Wilk para comparar el comportamiento del consumo eléctrico contra la normal cubana.
Para probar el supuesto de cómo se está comportando el consumo/donación con respecto a la norma cubana 7,56 Kw/donación, se analizaron datos mensuales desde el año 2017 hasta el 2021, para un registro de 60 observaciones. (Tabla 5).
Al ser el p-value menor que 0,05 se pone de manifiesto que el consumo por donación en este período es superior a la norma.
Cálculo de los modelos estadístico matemáticos de regresión polinomial
Para realizar la regresión no lineal se toman las medianas de los datos estadísticos del comportamiento del consumo eléctrico en los 5 años con respecto a la cantidad de donaciones. Se aplica el Método de los Mínimos Cuadrados a los datos obtenidos, mediante el uso del MatLab, se obtiene la tabla de los valores r2 (Bondad del Ajuste) modelos estadísticos – matemáticos de regresión polinomial de grado 1 hasta el 5. (Tabla 6).
Método de los Mínimos Cuadrados utilizado para calcular los coeficientes de un polinomio de grado n de la forma:
Sea el polinomio 
El polinomio de mejor ajuste 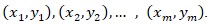
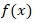
Matriz de las primeras derivadas de la función f(x) igualada a cero (Condición necesaria) para encontrar los coeficientes del polinomio que den valores mínimos de la función y = f(x), función II 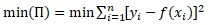
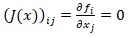
Condición suficiente para la obtención del mínimo local del error es: H f (x0) Matríz del Hesiano definida positiva.
Estos son los resultados de los 𝑟2 que da el Matlab en los diferentes grados polinomiales, tomamos el modelo estadístico - matemático polinomial de grado 3 que presenta el valor del residuo 𝑟2 de 0.6122 dado que los modelos polinomiales de mayor grado presentan más complicaciones en su análisis y las diferencias en significación son muy pequeñas.
En este caso el modelo estadístico – matemático polinomial de ajuste, calculado por el MatLab viene dado la ecuación.
y = 𝑝1 ∗ 𝑥3 + 𝑝2 ∗ 𝑥2 + 𝑝3 ∗ 𝑥 + 𝑝4
Donde el valor de los coeficientes obtenidos con un 95 % de confianza son: 𝑝1 = 0.0003457, 𝑝2 = −0.102, 𝑝3 = 5.013, 𝑝4 = 235.9
Coeficiente de las Bondad de ajuste R2 = 0.6122
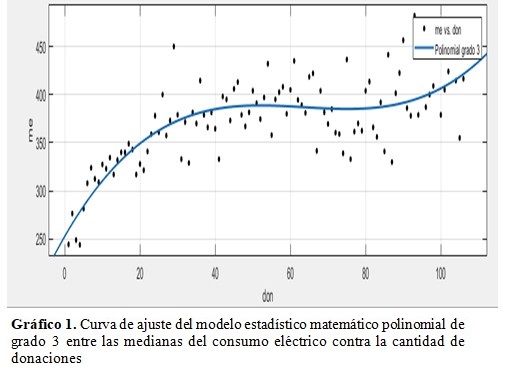
Se muestra el comportamiento del modelo estadístico matemático polinomial de ajuste de orden 3 con la nube de puntos. (Gráfico 1).
En el Grafico 1 se muestran los valores de consumo eléctrico (eje y) con respecto a las donaciones (eje x) que determina el modelo de regresión no lineal (curvilíneo) más conveniente a utilizar,
Se analizan diferentes regresiones: regresión logarítmica, exponencial, potencial, polinomial, entre muchas más.(9)
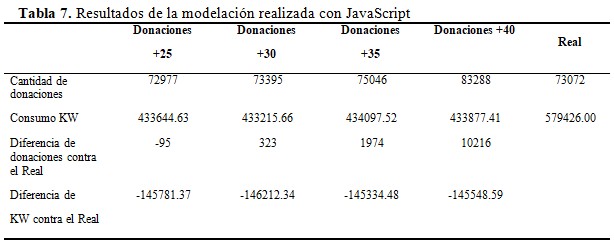
Para la obtención del Modelo estadístico matemático de Regresión que simule las donaciones con respecto al consumo eléctrico, se confeccionó un software en lenguaje de programación JavaScript,(10,11,12,13) el software simula la ecuación de regresión que no solo da el número de donaciones diarias, sino también el consumo eléctrico para esa donación. En la simulación se ejecutan 1551 veces (cantidad de muestras tomadas diariamente en los 5 años en el Banco de Sangre) y se generaron diferentes escenarios para observar su comportamiento, las corridas se dividen en diferentes números de donaciones diarias, durante el período de los 5 años, 25, 30, 35, y 40 donaciones por día.
La Tabla 7 compara los resultados con el real que existe en el banco desde el 2017-2021.
Los resultados de las 1551 corridas de días de donaciones, mostraron que 30 o más donaciones por día (+30) es el número óptimo de donaciones a realizar por día con respecto al menor valor del consumo eléctrico.
Con 25 o más donaciones hay menos donaciones en el ciclo de los 5 años y con 35 o más donaciones diarias el resultado es un número mayor de donaciones con un valor mayor del consumo energético en total a realizar, este número de donaciones es un poco más elevado que el real. En la modelación con 30 o más donaciones se obtuvo un ahorro de 146212.34 KW del ciclo de 1551 días de donaciones realizadas, según el modelo simulado, esto representa contra la norma 5.94 KW/Donaciones por debajo de la norma cubana de la resolución 299 del MINSAP de 7.56 KW/Donaciones.
DISCUSIÓN
A partir del estudio realizado se arriba a las siguientes conclusiones:
Se obtiene un modelo estadístico - matemático de regresión no lineal con la utilización del MatLab para el estudio del sistema de donaciones de sangre contra el consumo de energía eléctrica.
Se caracteriza el comportamiento aleatorio que sique la distribución de las donaciones en el Banco de Sangre.
Se formula un Modelo Estadístico - Matemático que permite simular el funcionamiento de las donaciones en el Banco de Sangre con respecto al consumo eléctrico y experimentar con diferentes condiciones de cantidad de donantes diarias.
Se formula y se resuelve un modelo de programación de donaciones diarias mínimas para iniciar el servicio de donaciones en el Banco de Sangre, que permitan que el consumo eléctrico sea correspondiente con la cantidad de donaciones y cumplan con la norma cubana 299 del MINSAP.
Se confeccionó un software, creado específicamente para este trabajo, programado en Jabscrip, para calcular el número de donaciones diarias, su consumo eléctrico y su correspondencia con la noma cubana 299 del MINSAP, se propone el número óptimo de 35 o más donaciones diarias con respecto al consumo eléctrico.
El trabajo constituye una herramienta que puede ser utilizado para la mejora de la planificación de las donaciones diarias, en la que no exista un elevado derroche de electricidad en el Banco de Sangre.
Conflicto de intereses
No existen conflictos de intereses.
Contribuciones de los autores
Conceptualización: Manuel Cortés Cortés.
Metodología: Manuel Cortés Cortés.
Investigación: David Lorenzo Calles.
Análisis formal: David Lorenzo Calles, Manuel Cortés Cortés.
Supervisión: David Lorenzo Calles, Manuel Cortés Cortés.
Redacción: David Lorenzo Calles, Manuel Cortés Cortés.
Redacción, revisión y edición: Manuel Cortés Cortés
Financiación
Universidad Carlos Rafael Rodríguez. Cienfuegos. Cuba.